Using New and Stable Wavelet Coefficients in Instrument Sound Analysis

UFPr Arts Department
Electronic Musicological Review
Vol. 6 / March 2001

EMR Home - Home - Editorial - Articles - Past Issues

USING NEW AND STABLE WAVELET COEFFICIENTS IN INSTRUMENT SOUND ANALYSIS

João Cândido Dovicchi

This paper explores the application of new wavelet coefficients to bassoon and French horn sound analysis. The coefficients were constructed based on musical chromatic intervals and applied to the dilation equation to yield wavelet filter coefficients. The examples provided compare recorded and inverse transformed signals, which suggests the potential of the model when applied to sound analysis of data segments of interest.

Introduction

Sound synthesis methods that can reproduce acoustic instruments are based on analysis methods that provide computationally efficient transfer functions. In addition to their application in the reproduction of natural sounds, powerful analysis tools can be used to produce new sounds that can be used in electroacoustic music composition.

During the last two decades there has been great interest in functions that, as transforms, can be used in the analysis and synthesis of sound events. Amongst them, wavelets have caught the attention of scientists in many areas who search for new methods for signal analysis, filtering and reconstruction [1,18]. Wavelets have been used in image processing [1,2], restoration of recordings [13], seismology [14], and economy [11], amongst other subjects. As the Discrete Fourier Transform (DFT), the Discrete Wavelet Transform (DWT) is a set of linear operations performed on a 2ⁿ vector that yields another vector of the same size; it is an orthogonal function, therefore inversible like other transfoms. The idea in wavelet filtering is to use variable scales in time and frequency domains which can sparsely represent each data set when a proper wavelet function is applied. This means that each data interval can be amplified for further analysis of each component in its corresponding scale.

Grossman and Morlet's work [12] at the end of the 70's played an important role in engineering and mathematics research into the bases for harmonic analysis in other function spaces. Searching for square integrals of (ax + b), they tackled the problem of constructing a base for L² (R)¹ from a discrete set of ax+b. They showed that, if there is a function $\psi_{(a,b)}(t) \in \Re$ , then its elements can be used as an orthogonal base (see eq. 1). Alternatively, each finite energy data of a signal can be represented as a linear combination of $\psi_{(a,b)}(t)$ , and its coefficients can be represented by their scalar products $\int_{-\infty}^{\infty} \psi_{(a,b)}(t) dt$ , which measure the fluctuation of the signal f(t) around b on scale a.

$\begin{displaymath} \psi_{(a,b)} (t)=\frac{1}{\sqrt{a}} \cdot \psi \left( \frac{t-b}{a} \right), \qquad \quad a > 0, \qquad \quad b \in \Re. \end{displaymath}$

(1)

Meyer [17] has found a special smooth function which he called Wavelet due to its oscillation around the x axis. This function tends to zero at $\pm \infty$ and its discrete orbit yields a Hilbert base for L²(R) as well as an unconditional base for all the Banach spaces². Lemarié [15] has also used it to prove basic facts of the Calderón-Zigmund algebra, but it was only a few years ago that Daubechies [5] developed an algorithm to construct other wavelets for some particular spaces of functions, including orthonormal wavelets with compact support.

The advantage of DWT over DFT methods is that Fourier bases are frequency-dependent but not time-dependent, which means that small changes in the frequency domain produce changes all over the time domain. Wavelets depend on the frequency domain via dilation³ and on the time domain via translation, ⁴ which is an advantage. For a more detailed analysis please refer to [20].

DWT is the most recent solution to some of the DFT limitations, once it can solve the problem of specific event localization in a signal through scaling and modular windowing of the function. Wavelet transform functions allow a more compact representation in comparison with other transform methods and can be used for analysis, synthesis and compression of signals, images and other numerical analysis.

In recent research reports [7,9] we have presented a new set of coefficients based on a chromatic subdivision of the musical scale and shown its applicability to sound signals analysis. We have also presented some results of a combined method of signal processing using the Short Time Fourier Transform (STFT) to test results achieved with DWT [8].

Multiresolution Analysis

Multiresolution analysis (MRA) [6] can be undertaken through a scaling function $\phi$ which is a sequence of near subspaces V_j in L $^2[-\infty,+\infty]$ such that

$\begin{displaymath}\cdots V_{-2} \subset V_{-1} \subset V_{0} \subset V_{1} \subset V_{2} \subset \cdots \end{displaymath}$

and which satisfies the following properties:

1.: Density: $\cup_{j} V_{j}$ is dense in L $^2[-\infty,+\infty]$ .
2.: Separation: $\cap_{j} V_{j}=0$ .
3.: Scalability: $f(t) \in V_{j} \Longleftrightarrow f(2t) \in V_{j+1}$ for all integers j and arbitrary f.
4.: Orthonormality: function $\phi(t-k)$ for $k=0,\pm 1, \pm 2,\dots$ forms an orthonormal base for V₀.

The MRA $\{V_{j}\}$ is generated by the scaling function $\phi$ , where, for each j the subspace V_j is generated by $\phi_{k}^{j}$ , for $k=0,\pm 1, \pm 2,\dots$ . Since $\{\phi_{k}^{j}\}$ is an orthonormal basis in V_j for each $j=0,\pm 1,\pm 2,\dots$ , if we assume that $\phi \in V_{0} \subset V_{1}$ , then we can write:

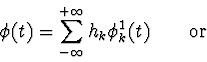$\begin{displaymath}\phi(t)=\sum_{-\infty}^{+\infty} h_{k} \phi_{k}^{1}(t) \qquad \mathrm{or} \end{displaymath}$

(2)

$\begin{displaymath} \phi(t)=\sqrt{2} \sum_{-\infty}^{+\infty} h_{k} \phi(2t-k) \mathrm{.} \end{displaymath}$

(3)

Equation 3 is called the dilation equation, and its coefficients h_k are the wavelet filter coefficients of the MRA⁵.

The Fourier transform of the dilation equation can be calculated from

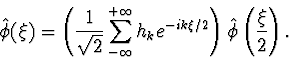$\begin{displaymath}\hat{\phi}(\xi)=\left( \frac{1}{\sqrt{2}} \sum_{-\infty}^{+... ...i/2} \right) \hat{\phi} \left(\frac{\xi}{2} \right) \mathrm{.} \end{displaymath}$

(4)

Wavelet Coefficients

As shown by Daubechies et.al. [6], the coefficients of a wavelet filter must satisfy the equation:

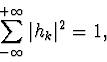$\begin{displaymath}\sum_{-\infty}^{+\infty} \vert h_{k}\vert^2=1 \mathrm{,} \end{displaymath}$

(5)

and, once $\Vert\phi\Vert=1$ [18], h_k can be written as

h_k	=	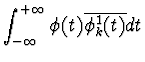$\displaystyle \int_{-\infty}^{+\infty} \phi(t) \overline{\phi_{k}^{1}(t)} dt$	(6)
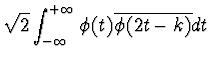	=	$\displaystyle \sqrt{2}\int_{-\infty}^{+\infty}\phi(t) \overline{\phi(2t-k)} dt$	(7)

The orthogonality of $\phi$ or

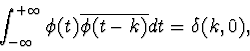$\begin{displaymath}\int_{-\infty}^{+\infty} \phi(t) \overline{\phi(t-k)} dt=\delta(k,0), \end{displaymath}$

(8)

where $\delta$ is the Kronecker symbol⁶, can be calculated from the dilation equation.

$\begin{displaymath} \sum_{m} \sum_{n} h_{m} \overline{h_{n}} 2 \int_{-\infty}^{+... ...hi(2t-m) \overline{\phi(2t-2k-n)} dt=\delta(k,0)c \mathrm{.} \end{displaymath}$

(9)

Equation 9 can be expressed as $\sum_{m}$ or

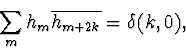$\begin{displaymath}\sum_{m} h_{m} \overline{h_{m+2k}}=\delta(k,0) \mathrm{,} \end{displaymath}$

(10)

where k is an arbitrary integer⁷. If we assume that $\phi$ can be integrated and

$\begin{displaymath} I=\int_{-\infty}^{+\infty} \phi(t) dt \neq 0 \end{displaymath}$

(11)

we can integrate both sides of the dilation equation as

$\begin{displaymath} \begin{array}{ccc} \int_{-\infty}^{+\infty} \phi(t) dt &=&... ... h_k \int_{-\infty}^{+\infty} \phi(s) ds \end{array}\mathrm{.} \end{displaymath}$

(12)

Thefore, if we keep the first and the third parts of equation 12 and divide the expression by I (see equation 11), we obtain:

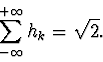$\begin{displaymath}\sum_{-\infty}^{+\infty} h_k=\sqrt{2}. \end{displaymath}$

(13)

Method

We carried out the analysis of recorded notes of French horn and bassoon, focusing on the attack and steady-state transients. Analyses were carried out as described in [7]. In short, this entailed: application of the DWT, splitting of the low-pass window, thresholding, high-pass recovery and inverse DWT. Using Pollen's parametric equations [19] we calculated two sets of wavelet coefficients (chroma4 and chroma6). Cody and Daubechies [3,6] also describe the calculation of the space parameter⁸ of a system h_n for $-2 \leq n \leq 3$ , which can be obtained from:

h_-2	=	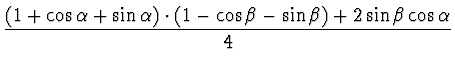$\displaystyle \frac{( 1+\cos \alpha+\sin \alpha) \cdot (1-\cos \beta - \sin \beta ) + 2 \sin \beta \cos \alpha }{4}$	(14)
h_-1	=	$\displaystyle \frac{( 1-\cos \alpha + \sin \alpha ) \cdot (1+\cos \beta - \sin \beta ) - 2 \sin \beta \cos \alpha }{4}$	(15)
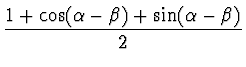h₀	=	$\displaystyle \frac{1 + \cos(\alpha - \beta) + \sin(\alpha - \beta)}{2}$	(16)
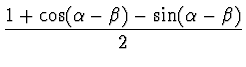h₁	=	$\displaystyle \frac{1 + \cos(\alpha - \beta) - \sin(\alpha - \beta)}{2}$	(17)
h₂	=	1 - h_-2 - h₀	(18)
h₃	=	1 - h_-1 - h₁	(19)

Using $\alpha=2^{1/12}$ and $\beta=0$ we have a set of 4 coefficients we named chroma4, and using $\alpha=2^{1/12}$ and $\beta=2^{2/12} - \alpha$ we have a set of 6 coefficients we named chroma6.

Signals were converted from RIFF/WAV format to a text numeric vector and splitted into files with 4096 samples from the attack and the steady-state parts. Using a similar algorithm as described by Mallat [16], each transformation was splitted into a high-pass and low-pass segment. The high-pass was discarded and the low-pass was used as input to a new transformation. We studied the signal reconstruction from the low-pass segment for each step (decimated by a factor of 2, 4 and 8) until the this segment could yield a signal reconstruction without significant loss of quality. Figure 1 shows the high-pass segments for each decimation. The results of the transform and the recovery of the signal were compared to the original sound using STFT analyses.

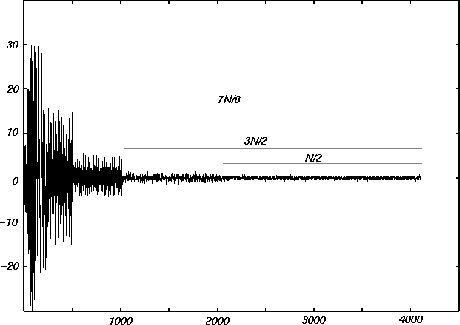$\begin{figure}\begin{center} \epsfig{figure=cortes.ps,width=4.5in}\end{center}\end{figure}$

Figure 1: Example of the splitting algorithm of the transformed signal (the low-pass segment was used as scaling function).

Wavelet coefficients were used as low-pass and high-pass complementary filters that can be written as a Finite Impulse Response (FIR) filter by the equation:

$\begin{displaymath}y_k=\sum_{t=-\infty}^{\infty} c_{(k-t)} \cdot x_t \end{displaymath}$

(20)

where y_k is the output of a signal x_k convolved with c_(k-t).

Results

Although we have analysed all the notes of each instrument, we present examples for low fundamental frequency sounds of the bassoon and characteristic sounds of the French horn, since these sounds are more difficult to analyse using traditional Fourier methods. Low sounds of the bassoon present an overlap in their spectra due to the small difference between its harmonics, which cannot be well visualized in Fourier spectra. Additionally, the high energy harmonics are found around 500 Hz and, considering low sounds, this can be located far away from the fundamental frequency. Sounds of the French horn were choosen because of their harmonic richness.

The harmonic energies of each segment refer to a 100-samples size window of the STFT of the attack and the steady-state sections of its envelope. Windows are represented by t_n and values are absolute magnitude around n for $n={1 \dots 5}$ . Table 1 shows harmonic frequency energies of each window (t₁, ... t₅) obtained from the original recorded sound of a french horn playing an A and the ones yielded by recovered signals after transformation with chroma4 and chroma6. Sound signals reconstructed after using chroma4 and chroma6 wavelet transforms showed no difference to the original recorded sound for all notes of the french horn. As we have shown in an earlier study [8], when compared to other DWT coefficients (Haar, Daubechies4 and Coiflet), these coefficients yield better results.

Table 1: Sound of French horn playing an A ( $\sim 440$ Hz), comparison of original sound and recovered after transformation with chroma4 and chroma6. Steady-state, MAG₍max)=6.2920 at 441.4 Hz.

signal	frequency	t₁	t₂	t₃	t₄	t₅
original	441.43	0.6996	3.3319	5.7855	6.2912	5.7680
Chroma4	441.43	0.6996	3.3321	5.7860	6.2918	5.7701
Chroma6	441.43	0.6988	3.3283	5.7787	6.2824	5.7616
original	882.86	0.2538	1.2277	2.1117	2.2623	2.0957
Chroma4	882.86	0.2535	1.2264	2.1091	2.2591	2.0941
Chroma6	882.86	0.2542	1.2278	2.1094	2.2582	2.0922
original	1324.29	0.0632	0.3432	0.6033	0.6418	0.6201
Chroma4	1324.29	0.0630	0.3427	0.6028	0.6413	0.6182
Chroma6	1324.29	0.0638	0.3451	0.6057	0.6441	0.6211
original	1765.72	0.0407	0.2009	0.3366	0.3471	0.3383
Chroma4	1765.72	0.0410	0.2016	0.3375	0.3484	0.3355
Chroma6	1765.72	0.0406	0.2008	0.3367	0.3476	0.3385
original	2207.15	0.0320	0.1362	0.2057	0.2035	0.1956
Chroma4	2207.15	0.0322	0.1363	0.2052	0.2030	0.1916
Chroma6	2207.15	0.0319	0.1357	0.2042	0.2030	0.1922
original	2648.58	0.0082	0.0281	0.0364	0.0377	0.0451
Chroma4	2648.58	0.0085	0.0297	0.0387	0.0399	0.0451
Chroma6	2648.58	0.0083	0.0286	0.0364	0.0369	0.0421
original	3090.01	0.0074	0.0250	0.0284	0.0220	0.0169
Chroma4	3090.01	0.0074	0.0263	0.0306	0.0237	0.0188
Chroma6	3090.01	0.0075	0.0254	0.0274	0.0225	0.0154
original	3531.45	0.0011	0.0089	0.0156	0.0148	0.0182
Chroma4	3531.45	0.0016	0.0097	0.0162	0.0158	0.0211
Chroma6	3531.45	0.0012	0.0102	0.0166	0.0136	0.0218
original	3972.88	0.0036	0.0108	0.0088	0.0049	0.0083
Chroma4	3972.88	0.0037	0.0125	0.0109	0.0058	0.0085
Chroma6	3972.88	0.0039	0.0117	0.0094	0.0067	0.0056
original	4414.31	0.0017	0.0021	0.0008	0.0007	0.0024
Chroma4	4414.31	0.0016	0.0018	0.0012	0.0006	0.0046
Chroma6	4414.31	0.0013	0.0021	0.0012	0.0008	0.0045
original	5297.17	0.0013	0.0018	0.0017	0.0024	0.0053
Chroma4	5297.17	0.0011	0.0019	0.0022	0.0022	0.0048
Chroma6	5297.17	0.0013	0.0015	0.0001	0.0020	0.0046
original	5738.60	0.0024	0.0047	0.0032	0.0060	0.0069
Chroma4	5738.60	0.0025	0.0056	0.0033	0.0065	0.0091
Chroma6	5738.60	0.0027	0.0063	0.0045	0.0074	0.0085
original	6180.03	0.0012	0.0024	0.0015	0.0012	0.0024
Chroma4	6180.03	0.0010	0.0030	0.0023	0.0014	0.0033
Chroma6	6180.03	0.0014	0.0031	0.0009	0.0015	0.0037

Table 2 shows the frequency and magnitude of the harmonic with highest energy of the bassoon sound, as it was the one which presented some difference. We noticed a slight variation in sound reconstruction, but this does not represent a change in sound quality. A comparison between the graphical representations of the original and recovered sound after 4 step transforms using chroma4 and chroma6 coefficients (Figures 2, 3 and 4) suggests that no real difference exists between those sounds and that those coefficients yield acceptable results in low-frequency sounds analysis as well.

Table 2: Comparison of frequency energies of a bassoon playing a C ( Hz). Attack section MAG_(max)=1.6760 at 463.0 Hz. Values with significant differences in magnitude ( $\delta \geq 0.002$ ) are in bold face characters.

signal	frequency	t₁	t₂	t₃	t₄	t₅
original	323.00	0.0150	0.1672	0.4218	0.5365	0.4915
Chroma4	323.00	0.0150	0.1674	0.4225	0.5377	0.4926
Chroma6	323.00	0.0147	0.1662	0.4206	0.5349	0.4910
original	387.60	0.0225	0.2622	0.6790	0.8621	0.8048
Chroma4	387.60	0.0225	0.2623	0.6799	0.8631	0.8054
Chroma6	387.60	0.0222	0.2605	0.6768	0.8591	0.8028
original	452.20	0.0266	0.3308	0.9116	1.1945	1.2027
Chroma4	452.20	0.0266	0.3308	0.9116	1.1938	1.2025
Chroma6	452.20	0.0262	0.3286	0.9083	1.1899	1.1980
original	516.80	0.0213	0.2661	0.6794	0.7578	0.8655
Chroma4	516.80	0.0213	0.2659	0.6783	0.7561	0.8652
Chroma6	516.80	0.0210	0.2642	0.6768	0.7556	0.8619
original	581.40	0.0116	0.1458	0.3637	0.4034	0.4793
Chroma4	581.40	0.0116	0.1454	0.3627	0.4031	0.4793
Chroma6	581.40	0.0115	0.1455	0.3635	0.4017	0.4770


$\begin{figure}\begin{center} \epsfig{figure=result2.ps,width=4.5in}\end{center}\end{figure}$

Figure 2: Recorded sound spectrum of the attack section of a bassoon playing a low C ( $\sim 64.60$ Hz).

$\begin{figure}\begin{center} \epsfig{figure=result3.ps,width=4.5in}\end{center}\end{figure}$

Figure 3: Recovered sound spectrum of the attack section of a bassoon playing a low C ( $\sim 64.60$ Hz) after transformation using chroma4 wavelet coefficient.

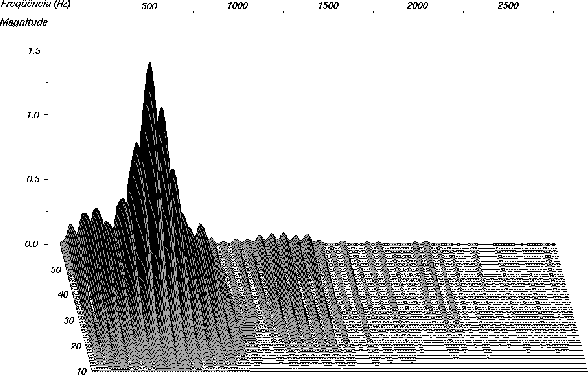$\begin{figure}\begin{center} \epsfig{figure=result4.ps,width=5in}\end{center}\end{figure}$

Figure 4: Recovered sound spectrum of the attack section of a bassoon playing a low C ( $\sim 64.60$ Hz) after transformation using chroma6 wavelet coefficient.

We have also tested transforms with more than four steps and compared them to other wavelet coefficients (e.g. Haar, Daubechies4, Daubechies6 and Coiflet) and we have obtained some sound distortion. Analysis showed a pattern repetition of the centroid section in harmonic basis. This is more characteristic when using chroma4 coefficients and sugests we can use it to study instrument sound signatures or quality once we stablish some standards. We are carrying out further research into this issue.

Conclusion

The set of new wavelet coefficients proved to be stable and yields good results for instrument sound analysis. For all tested signals, results were very consistent allowing the decomposition, analysis and reconstruction of sound signals as well as very accurate identification of sound events at specific data segments of interest. Compression of signals needs to be studied to verify its application on this domain. Once transforms and data recovering are precise, using windowing methods and convolution with those coefficients can also ease the spectral analysis and provide means for the calculation of transfer funtions to be used in synthesizers and music composition. The study of the distortion produced with transformations above 8 steps of the MRA needs to be carried out to verify its applicability in sound centroid analysis and quality control of acoustic instrument construction.

Bibliography

[1]: BRADLEY, J. N.; BRISLAWN, C. M. & HOPPER, T. The FBI wavelet/scalar quantization standard for grey-scale fingerprint image compression. In: Visual Information Processing, II Vol., Proceedings of SPIE, Orlando, Florida.: SPIE, pp. 293-304, 1993.
[2]: BRISLAWN, C. M. Fingerprints go digital, Notices of the A.M.S., 42, Nr. 11 pp. 1278-1283, 1995.
[3]: CODY, M. A. The Wavelet Transform Beyond Fourier Transforms. Dr. Dobb's Journal, M & T Publishing Inc., April, 12 pp., 1992.
[4]: DAUBECHIES, I. Where do Wavelets Come From? -- A Personal Point of View. Proc. of IEEE, vol. 84 no. 4, 1996.
[5]: DAUBECHIES, I. Discrete series of coherent states and their use in signal analysis. Tech. Rep., Couranmt Institute of Mathematical Sciences, New York, n.d.
[6]: DAUBECHIES, I. Ten Lectures on Wavelets, CBMS-NFS Regional Conf. Series in Appl. Math., Vol 61. Society for Industrial and Applied Mathematics, Philadelphia, PA, 1992.
[7]: DOVICCHI, J. C. Novos Coeficientes Wavelets Baseados em Intervalos Musicais para Análise de Timbres de Instrumentos Acústicos, PhD Thesis, Universidade Federal de Uberlândia, 183 pp., 1999.
[8]: DOVICCHI, J. C.; CARRIJO, G. A.; LIMA, L. Fourier Transforms and Wavelets: a Combined Technique for Musical Signal Analysis. Proceedings of the Conference on Mathematical and Computational Methods in Music, Diderot'99., Universidade de Viena, Viena, 13 pp., 1999.
Available at http://www.demac.ufu.br/lab/papers/fft-wav.ps
[9]: DOVICCHI, J. C.; CARRIJO, G.; LIMA, L. Music Based Coefficients for Wavelets Transform: a Contribution to Musical Signal Analysis. Accepted at the 108 $^{\underline{th}}$ Convention of the Audio Engineering Society, 108th AES Convention, Paris, Feb. 2000.
[10]: COOLEY, J. W.; TUKEY, J. W. An Algorithm for the Machine Calculation of Complex Fourier Series. Math of Computation, vol. 19, pp. 297-301, 1965.
[11]: GREENVLATT, S. A. Wavelets in econometrics. The Maple Tech. Newsletter, pp. 10-16, 1994.
[12]: GROSSMAN, A. e MORLET, J. Decomposition of Hardy functions into square-integrable wavelets of constant shape. SIAM J. Math. Anal., vol. 15, pp. 723-736, 1984.
[13]: KOBAYASHI, M. Listening for defects: wavelet-based acoustical signal processing in Japan. SIAM News, (March), p. 24, 1996.
[14]: KOBAYASHI, M. Netting namazu: earthquakes and Japanese wavelet research SIAM News, (July/August), p. 20, 1996.
[15]: LEMARIÉ, P. G. Continuité sur les espaces de Besov des opérateurs définis par les intégrales singulières. Annales de l'Institute Fourier, appud: Mallat, S.G. (1989). IEEE Trans. on Pattern Analysis and Machine Intelligence, vol. 11, pp. 674-693, 1989.
[16]: MALLAT, S. A. Theory for MultiresolutionSignal Decomposition: The Wavelet Representation. IEEE Trans. Pattern Anal. Machine Intelligence, 11, pp. 674-693, 1989.
[17]: MEYER, Y. Principe d'incertitude, bases hilbertiennes et algèbres d'operateurs. Séminaire Bourbaki, vol. 662, 1986.
[18]: MEYER, Y. Wavelets Algorithms & Aplications, trad. Robert D. Ryan, 2^a Ed. (1994), Philadelphia: SIAM - Society for Industrial and Applied Mathematics, 1993.
[19]: POLLEN, D. Parametrization of compactly supported Wavelets, Tech. Report, Aware Inc., 1989.
[20]: STRANG, G. Wavelet transforms versus Fourier transforms, Bulletin of the A.M.S., 28, No. 2 (April), pp. 288-305, 1993.

Notes

...)¹: L²(R), is called Hilbert space, a sequence $x=(\lambda_k)$ of complex numbers $\lambda$ , where: $\lambda=(\alpha + i\beta), \qquad \alpha,\beta \in \Re$ , of square sums: $\sum_{1}^{\infty} \left\vert \lambda_k \right\vert < \infty$ .
... spaces ²: set of continuous linear applications on a normed space L², where: $\Lambda (L)={\bf T} : L \rightarrow L$ .
... dilation ³: Function that takes a vector and returns another multiplied by a scalar: $\overrightarrow{v} \rightarrow \lambda \overrightarrow{v}$ , where $\lambda$ is any scalar and $\overrightarrow{v}$ any vector in any space.
... translation ⁴: Function that sums a constant vector $\overrightarrow{k}$ to any other: $\overrightarrow{v} \rightarrow \overrightarrow{k} + \overrightarrow{v}$ , where $\overrightarrow{v}$ and $\overrightarrow{k}$ are vectors in any space.
... MRA ⁵: The characterization of scaling functions is a bit more complicated than sequences of complex numbers of the wavelet filter. Once we calculate the wavelet coefficients, the scaling function $\phi$ can be obtained from equation 3.
... symbol ⁶: A function is said to have a $\delta$ Kronecker when it has only two values 0 and 1.
... integer ⁷: Note that $\sum_{m} \vert h_{m}\vert^2=1$ is a special case of k=0.
... parameter ⁸: A space parameter is a set of solutions that map a set of functions into one or more variables or parameters

Acknowledgements

This research was sponsored by the Conselho Nacional de Pesquisa (CNPq), Universidade Federal de Uberlândia (UFU), Programa Institucional de Bolsas de Iniciação Científica (PIBIC/CNPq). We also thank Centro de Processamento de Alto Desempenho de Minas Gerais (CENAPAD-MG), where great part of this work was undertaken.

João Cândido Dovicchi is an Assistant Professor at the Federal University of Uberlândia and a Researcher at the Center for Advanced Sonic Computing (NACS/UFU)