
| Revista eletrônica de musicologia |
||||
| Volume XII - Março de 2009 |
||||
home . sobre . editores . números . submissões
Analyzing the melodic structure of a North Indian raga: A Statistical Approach
Soubhik Chakraborty1, Kolla Krishnapriya2, Loveleen3, Shivee Chauhan 4, and Sandeep Singh Solanki5
Abstract
A raga is a melodic structure comprising of fixed notes and a set of rules characterizing a certain mood conveyed through performance. In the present article, a sound statistical basis is provided for analyzing the melodic structure of North Indian ragas using the raga Multani as a case study. Similarity measure is calculated with the help of correlation coefficient between shapes of melodies of equal length. Significance of a melody is obtained by multiplying the length of the melody and its number of occurrences in the musical piece, which is monophonic, under investigation. The analytical results are quite encouraging.
Key words:
Melody, segment, shape, translation, inversion, significance, similarity
1. Introduction
We first provide some fundamental definitions crucial to our analysis.
Definition1: Melody may be mathematically defined, without sacrificing the musical meaningfulness, as a sequence of notes, “complete” in some sense as determined by music theory, taken from a musical piece. A melody need not be a complete musical sentence. It suffices if it is a complete musical phrase. In the absence of completeness, it is very difficult to assess its meaningfulness or the “feel good” part in musical sense. The present paper makes a melodic study of the structure of Multani, an important North Indian raga. A raga may be defined as a melodic structure with fixed notes and a set of rules characterising a certain mood conveyed by performance. The advantage of analyzing the structure is that the results are fairly general while performance analysis is artist dependent. Moreover, the analysis can be done with a paper and a pen but knowledge of Indian music theory is essential. The other side of the coin is that performance gives several other characteristics of a note like duration, onset and loudness which can be meaningfully applied in the analysis. The transitory and non-transitory pitch movements taking places between the notes are also crucial. Readers interested in performance analysis of Indian classical music are referred to [1], [2] and [3].
Definition2: A segment is a sequence of notes which is a subset of a melody but is itself incomplete.
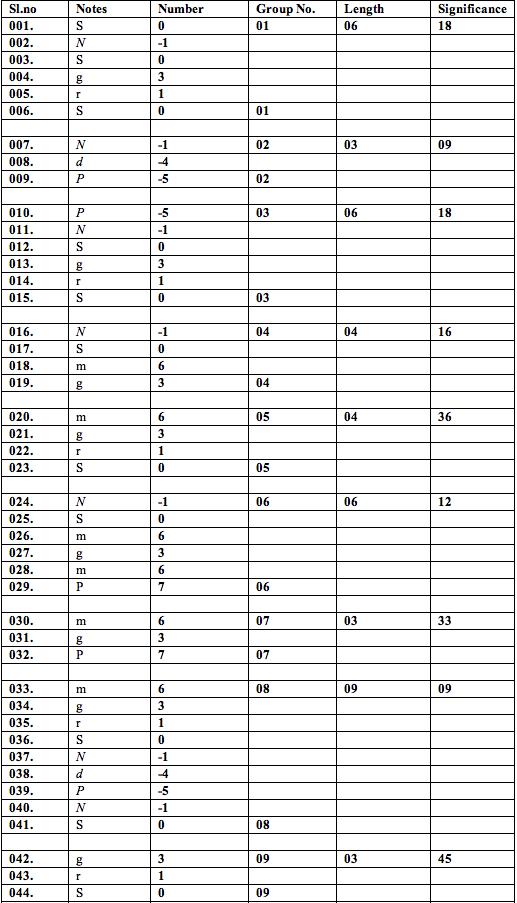
For example, in the present raga Multani, the note sequence {Sa, Ni, Sa, Ga (komal), Re (komal), Sa} or simply {S, N, S, g, r, S} is a melody while {S, N, S, g} is a segment. (See the abbreviations below table 1)
Table 1: Reference Standard Scale:

Remark: In table 1 above it is understood that the tonic Sa is at C. The twelve notes in the middle octave can be represented by the numbers 0 to 11 respectively. Sa of the next higher octave is assigned the number 12 etc while Ni (sudh) of the lower octave (before middle) is assigned the number -1 etc.
Abbreviations:-
The letters S, R, G, M, P, D and N stand for Sa (always Sudh), Sudh Re, Sudh Ga, Sudh Ma, Pa (always Sudh), Sudh Dha and Sudh Ni respectively. The letters r, g, m, d, n represent Komal Re, Komal Ga, Tibra Ma, Komal Dha and Komal Ni respectively. A note in Normal type indicates that it belongs to middle octave; if in italics it is implied that the note belongs to the octave just lower than the middle octave while a bold type indicates it belongs to the octave just higher than the middle octave.
We provide a few more definitions and the analysis follows accordingly.
Definition3: Length of a melody or its segment refers to the number of notes in it.
For example, the length of the Multani melody {S, N, S, g, r, S} is 6.
Definition4: Significance of a melody or its segment (in monophonic music such as Indian classical music) is defined as the product of the length of the melody and the number of times it occurs in the musical piece. Thus both frequency and length are important factors to assess the significance of a melody or its segment. The term has a more technical definition in polyphonic music [4].
Definition5: Shape of a melody is the difference of successive pitches of the notes in it represented by the numbers as given above.
Thus the Multani melody {S, N, S, g, r, S} would be represented by {0, -1, 3, 1, 0} and its shape is {-1, 4, -2, -1] upon taking successive differences of pitch from right to left.
Definition6; Two melodies are in translation if the correlation coefficient r of their shapes equals +1.
Definition7: Two melodies are in inversion if the correlation coefficient of their shapes equals -1.
Definition8: Two melodies are called different if the correlation coefficient of their shapes approaches 0 in magnitude. Thus r here is a measure of similarity between melodies. Mazzola [5] and Buteau [6] have investigated similarity by proximity and similarity by symmetry in combination.
Remark: Since correlation coefficient is a number between -1 and +1, fractional values approaching -1 or +1 or even zero can be interpreted likewise based on the above mentioned definitions. Significance of a correlation coefficient can be tested using t test. If r is the value of correlation coefficient and n be the number of pairs of observations (here successive differences), we calculate the statistic t=r√(n-2)/√(1-r2). If the absolute value of t, exceeds the table value of t at 5% level of significance (say) and (n-2) degrees of freedom, then the value of r is significant at 5% level otherwise insignificant. Here it is assumed that the n pairs are coming from a bivariate normal distribution (in our case n-2 will mean two subtracted from the number of elements in the melody shapes or equivalently 3 subtracted from the melody lengths).
The formula for r is covariance (x, y)/√{sd(x) sd(y)} where sd=standard deviation. Covariance(x,y) can be computed easily as {Sum(xy)}/n-mean (x)*mean (y). sd(x)=√[{Sum(x*x)}/n-mean (x)*mean( x)] and similarly for sd(y).
Basic and typical features of raga Multani are given in the appendix. Readers knowing western music but new to Indian music are referred to [7]. More literature on Indian music can be found in [8].
2. Statistical Analysis
The analytical results have been tabulated for convenience as follows.
RAGA MULTANI
Table 2: Melody groups and their significance





Table 3: comparison of 3 note melody phrases in pairs **:

**means the groups shown above are trivially significant as the ‘r’ values are 1 and -1 because a straight line is always defined uniquely for a pair of points in two dimension. So the only interest is the sign in this case.
Table 4: Comparison of 4 note melody phrases in pairs:

Table 5: Comparison of 5 note melody phrases in pairs:

Table 6: Comparison of 6 note melody phrases (covariance and correlation)

Table 7: Comparison of 9 note melody in pairs:

*infàinfinity
d.f. -> degrees of freedom
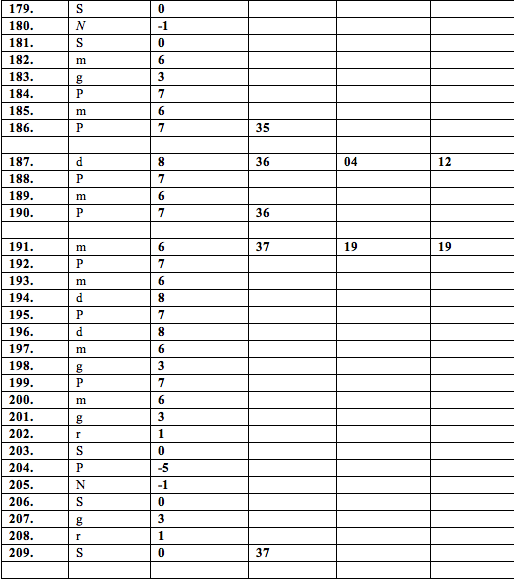
We have also analyzed segments apart from melodies. Here are some results.
Table 9: significance of 3 note melodies and segments
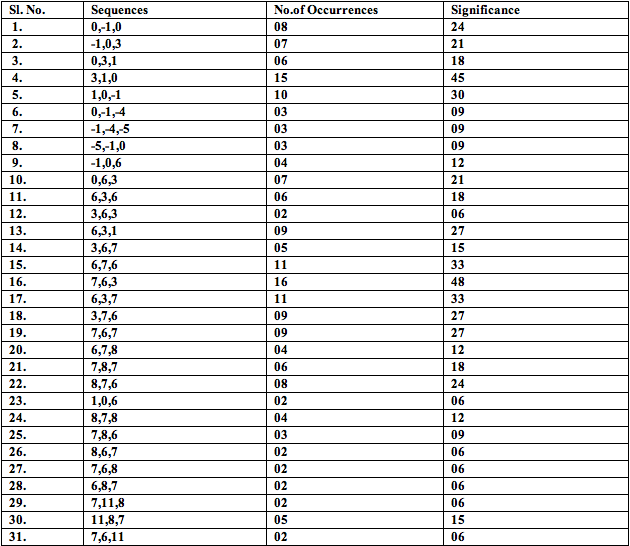
Table 10; sifnificance of 4 note melodies and segments
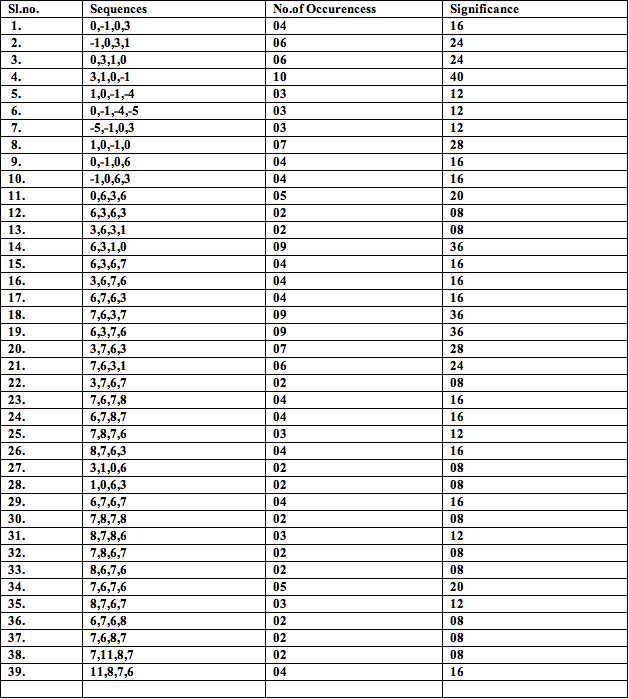
Table 11: Significance of 6-note melodies and segments:
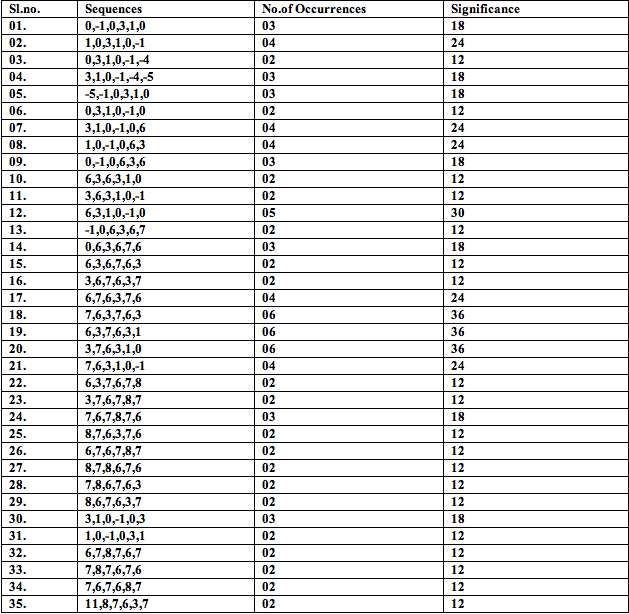
Table 12: Significance of 9-note melodies and segments:

Table 13: Significance of 10-note melodies and segments:
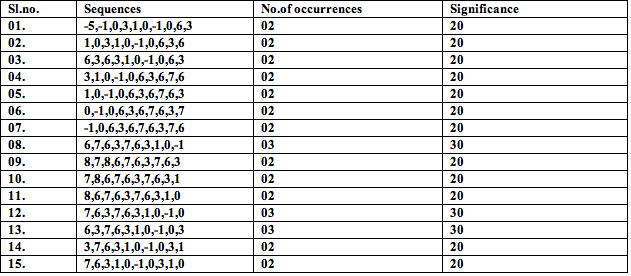
Remark: Melodies absent in the tables 9-13 have occurred only once. For such melodies, refer to table 1.
Conclusion
The reader must have noticed that in table 1, some melody groups were repeated. For instance, melody groups 5 and 20 are identical. Summarizing the results only for distinct melody groups yields table 14.
Table 14: Distinct melody groups and their significance in Multani

Remark: The highest significance 52 corresponds to a melody phrase of two notes only. Although we allowed it to compete with the more complete melodies (of at least three notes) so as to maintain continuity in the sequence of notes so far as formation of melody groups is concerned, our analysis suggests how even a very short melody phrase, which is more a segment rather than a full melody, can be important in a raga.
A question that is of interest is: as we move from one instance to another, do the probabilities of the different notes in the raga remain fixed or they vary on the whole? In other words, if we consider them fixed which is what should happen if the model is multinomial, must we not verify its goodness of fit? With this objective in mind, we split the note sequence in two groups, maintaining the sequence with the first 105 notes constituting group I and the next 104 notes, group II. By multiplying the relative frequencies (number of occurrences of pitch) of the notes over the entire sequence with the total frequency in a specific group, we could easily compute the expected frequencies of the notes in that group. This would be compared with the observed frequencies of the notes in the corresponding group using a Chi-Square test.
We have some interesting results (tables 15-17).
Table 15: No. of occurrences of Multani notes in the whole sequence

or all the notes in a group and this follows Chi-Square distribution with 7-1=6 degrees of freedom (one degree of freedom being lost due to the restriction that the sum of observed frequencies must equal the sum of expected frequencies)
For the first group, calculated chi-square = 5.3805
For the second group, calculated chi-square = 5.4318
Both these values are less than the table value of Chi-Square at 6 degrees of freedom and 5% level of significance which is 12.592. Hence the test statistic values are insignificant. So we can assume that the probabilities of the notes are not changing considerably on the whole as we move from one instance to the next. The phrase on the whole must be stressed in that the notes, strictly speaking, are not quite independent. In fact, using rigorous statistical analysis, it can be shown that an ARIMA model of lag one nicely represents the melodic structure of the present Multani sequence thereby validating a first order Markov chain [11]. [Concluded]
APPENDIX
RAGA MULTANI [9]
Multani is among the 'big' Ragas, highly regarded by the afficionado of vocal music for its weighty mien and wide melodic compass. Although its basic swaric material is drawn from the Todi thAT - S r g m P d N - it carries no hint or trace of the Todi Raganga. Multani has a highly evolved and independent swaroopa all its own.
Let us examine the Raga lakshaNAs. To recap the notation convention: a swara enclosed in brackets represents a kaNa (grace) to the swara immediately following it. The single quote ' on a swara situates it in the mandra saptaka, the double quote " situates it in the tAra saptaka.
S, N S g (S)r(N)S
Both r and d are dropped in Arohi prayogas; the avaroha is sampoorNa. The peculiar ucchAraNa (intonation) of r mediated by a kaNa (grace) of S is vital to Multani. Recall the vastly different behavior of Todi in this region, with its deergha r and an intimate coupling with g. An inopportune nyAsa on r spells the kiss of death for Multani. Further divergence between Todi and Multani in matters concerning g is suggested in the next tonal strip.
N S (m)g m P, m P (m)g, m g (S)r(N)S
Characteristic of Multani is the Arohi ucchAraNa of g: it is tugged with m as in (m)g (m)g m P. Since g is approached from m, it has the effect of raising the shruti of g to a location above its nominal komal value. This in turn elevates the shruti of r. These microtonal nuances are later demonstrated tellingly by Pandit Ramashreya Jha "Ramrang." The teevra madhyam in Multani is very close to the pancham, in the latter's penumbra, as it were.
P, (m)g P, P (P)d(m)P, P (m)g, m g m g (S)r(N)S
The treatment of d is congruent to that accorded r. The purNAvritti (repetition) of m g in avarohi prayogas is a point of note. As is the langhan of m, occasionally from g to P and more often through a meeND-laden avarohi P to g. The importance of a powerful pancham to Multani should be evident by now.
(m)g m P N, N, S, S g (S)r(N)S
The uttarAnga launch proceeds thus, with a deergha N. The sharp m P N curve presents a source of discomfort to many a Khayal singer especially in the faster passages; the tendency to instead detour through m d N must be checked.
S, N S N d P, m P (m)g, m g m g (S)r(N)S
This sentence completes the overall avarohi picture.
Multani is considered the daytime counterpart of the nightly Raga Basant.
· The Rampur musicians of the Tansen tradition sing a g-laden version of the latter by the name Utari Basant.
Here is a summary of the fundamental features of this raga [10]:-
Raga: Multani
Thaat: Todi (Thaat is a kind of grouping of ragas according to the specific notes used)
Aroh (ascent): N S, g m P, N S
Awaroh(descent): S N d Pm g r S
Jati(another grouping of raga reflecting no. of distinct notes used in ascent-descent): Aurabh-Sampoorna
(5 distinct notes used in ascent, 7 in descent)
Vadi Swar (most important note): P
Samvadi Swar (second most important note): S
Prakriti (nature): restful
Pakad (catch): N S, m g, P g, r S
Nyas swars (Stay notes): S g P
Time of rendition: 3 PM to 6 PM
References
[1] S. Chakraborty, S. S. Solanki, S. Roy, S. Chauhan, S. S. Tripathy and K. Mahto,
A Statistical Approach to Modeling Indian Classical Music Performance:
arXiv:0809.3214v1 [cs.SD] [stat.AP]. http://arxiv.org/abs/0809.3214 (2008)
[2] S. Chakraborty, S. S. Solanki, S. Roy, S. S. Tripathi and G. Mazzola,
A Statistical Comparison of Performance Two Ragas (Dhuns) that Use the Same
Notes, Proceedings to the International Symposium on Frontiers of Research I
Speech and Music (FRSM2008), held at Sir C. V. Raman Centre for Physics and
Music, Jadavpur University, Kolkata on Feb 20-21, 2008 (p.167-171)
[3] S. Chakraborty, R. Ranganayakulu, S. Chauhan, S. S. Solanki and K. Mahto,
An interesting comparison between a morning raga with an evening one using
graphical statistics, Philomusica online (to appear)
[4] K. Adiloglu, T. Noll and K. Obermayer, A Paradigmatic Approach to Extract the
melodic Structure of a Musical Piece, Journal of New Music Research, 2006,
Vol. 35, no. 3, 221-236
[5] G. Mazzola, The Topos of Music, Birkhauser Basel, 2002
[6] C. Buteau, Reciprocity between presence and content functions on a motivic
composition space, Tatra Mount Mathematics Publications, 2001, Vol. 23, 17-45
[7] C. S. Jones, Indian Classical Music, Tuning and Ragas, http://cnx.org/content/m12459/1.6/
[8] N. A. Jairajbhoy, The rags of North India: Their Structure and Evolution,
London; Faber and Faber, 1971
[9] ekrasiya.blogspot.com/2007/09/raga-multani
[10] D. Dutta, Sangeet Tattwa (Pratham Khanda), Brati Prakashani, 5th ed, 2006(in
Bengali)
[11] S. Chakraborty, R. K. Shukla, S. S. Solanki, S. Chauhan, Loveleen and K.
Krishnapriya, On Analyzing the melodic structure of a North Indian raga
through an ARIMA model, Jour. of Mathematics and Music (submitted)
Authors 1Department of Applied Mathematics, BIT Mesra, Ranchi-835215, India
2, 3, 4, 5Department of Electronics and Communication Engineering, BIT Mesra, Ranchi-835215, India
*corresponding author’s email: soubhikc@yahoo.co.in (S. Chakraborty)