
| Revista eletrônica de musicologia |
||||
| Volume XII - abril de 2009 |
||||
home . sobre . editores . números . submissões
Shadowing Along the Maestro’s Rhythm
(A shadow Analysis of Indian percussion performance with metrical and melodic properties)
1Soubhik Chakraborty, 2Rayalla Ranganayakulu*
Scientific Research Department, ITC Sangeet Research Academy, Kolkata 700040, India
Abstract
Musicologists regard handclapping and African drumming as a motor activity where a hand or an arm is raised and then dropped (to strike the instrument in the latter case). According to Jay Rahn, one possible mechanism for the tacit motor mediation of attack points of onsets is the peaking of the gesture at the temporal midpoint of the two sounds. He calls the sequence of midpoints of the onsets of a rhythm the shadow of the rhythm. In the present paper we take a close look at the shadow graphs for sets of interval 10 seconds each considering the first three minutes of a seven minute tabla recording played by a renowned Indian musician. This is followed by metric and melodic analysis of the percussion performance.
Key words: Rhythm, {shadow, metrical, melodic} analysis
1. Introduction
Several musicologists have expressed the view that activities such as handclapping and African drumming are best understood as a motor activity where a hand or an arm is raised and then dropped (to strike the instrument in the latter case). According to Jay Rahn [1] one possible mechanism for the tacit motor mediation of attack points of onsets is the peaking of the gesture at the temporal midpoint of the two sounds. He calls the sequence of midpoints of the onsets of a rhythm the shadow of the rhythm. There is a beautiful piece of mathematics associated with the shadow rhythm as the question ?gwhat happens to the sequence when we continue to perform this operation on every rhythm resulting from the shadow of another??h turns out to be a fascinating geometrical problem. The interested reader is referred to Martin, Taslakian and Toussaint [2]. A review of [2] by the first author can be found in [3]. A short account is, however, supplied in the appendix to give this paper a sense of completeness. In the present paper we take a close look at the shadow graphs for sets of interval 10 seconds each considering the first three minutes of a seven minute tabla recording played by a renowned Indian musician. This is followed by metric and melodic analysis of the percussion performance. In melodic analysis the timbre parameters (tristimulus 1, 2 and 3, spectral brightness, odd and even parameters, irregularity, spectral centroid and spectral inharmonicity) [5 to 10] are being calculated from the spectrum of sound signals of tabla. The most important features for the melodic properties are spectral inharmonicity, irregularity, brightness and centroid [8, 9, and 10]. The pitch of each stroke and the attack time for each stroke was calculated. The correlation between the parameters was studied. Readers unfamiliar with tabla as a percussion instrument are referred to [12].
2. Shadow
Analysis While our study was purely empirical, the theoretical example of a shadow provided by Martin, Taslakian and Toussaint [2] is no less interesting. They have considered the Cuban tresillo rhythm given by A[?~ ?E ?E ?E ?E ?E ?~ ?E ?E ?E ?E ?E ?~ ?E ?E ?E ] Its shadow is evidently B[ ?E ?E ?E ?~ ?E ?E ?E ?E ?E ?~ ?E ?E ?E ?E ?~ ?E ] leading to the shadow rhythm C[?~ ?E ?E ?E ?E ?E ?~ ?E ?E ?E ?E ?~ ?E ?E ?E ?E ]. Here, ?ex ?e represents a beat in A but a shadow in B and C. A ?g.?h is a silence in A but in B and C it can correspond to a beat if it is midway between two shadows otherwise a silence. Fundamental frequencies of the beats against their onsets were obtained using the Solo Explorer 1.0 software, a wave to midi converter and automatic music transcriber. Below are given the best and worst straight line fits for these graphs in MS Excel 2003. Best and worst graphs for first minute: Fig. 1.1 Best graph (onset 50-60 seconds)

Fig. 1.2: Worst graph(onset 20-30 seconds)

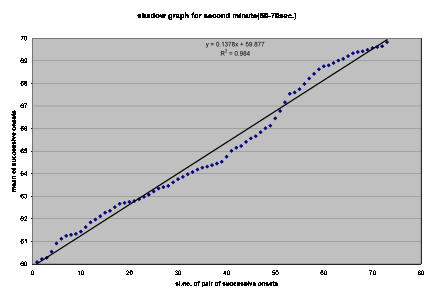
Best and worst graphs for second minute: Fig. 1.3 Best graph(onset 80-90 seconds)

Fig. 1.4 Worst graph (onset 60-70 seconds)
Best and worst graphs for third minute: Fig. 1.5 Best graph (onset 130-140 seconds)
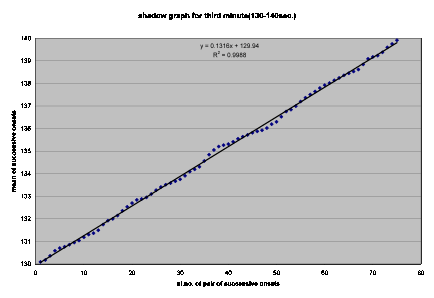
Fig. 1.6 Worst graph (onset 160-170 seconds)
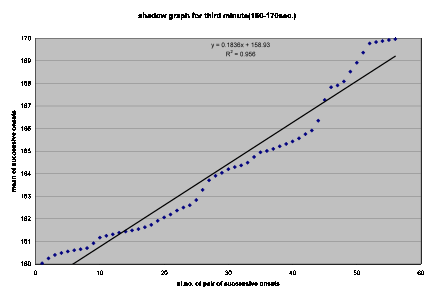
Interpretation of the shadow graphs:
The best shadow graphs are self explanatory. Although the graphs are spiral shaped the points can be well represented by straight lines. But for the worst ones, some explanation is required. While reviewing [2], the first author had made an important remark: ?gI don?ft think the idea of estimating peak onset time in the shadow case by averaging two successive onset times will always work. What if the musician gets out of the rhythm, plays a ?gfiller?h, and again regains the rhythm??h[3] In Indian percussion instruments such as the tabla, this ?gfiller?h is called bharav. One can speculate that the artist must have rendered some intricate bharav corresponding to the relevant portions of fig. 1.2, 1.4 and 1.6 (which we did not forget to confirm by actual listening!) leading to a clear deviation from the pattern obtained in the best cases. 3 Metric Analysis Metric (rhythmic) analysis is done next simply with inter onset interval time graphs (time between successive onsets) of beats. These graphs are drawn using MATLAB. For the endorsement of a rhythm, the inter onset interval times should be equal.
Fig. 2.1 Inter onset interval graph for the first minute:
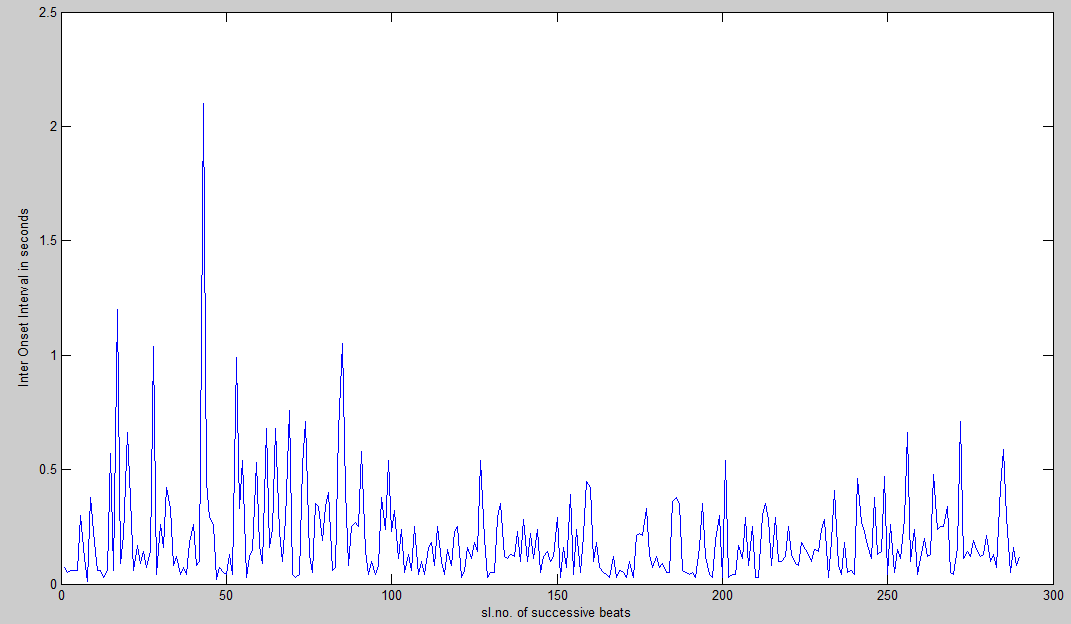
Fig. 2.2 Inter onset interval graph for the second minute

Fig. 2.3 Inter onset interval graph for the third minute:
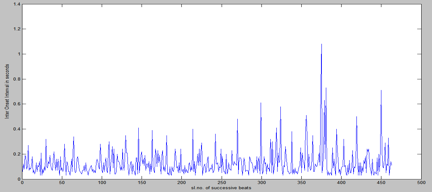
Interpretation of the inter onset interval time graphs:
The sudden high peaks here and there, which are not along a horizontal line, again implies a bharav or a ?gfiller?h but here the graph gives the actual beats struck by the artist during the bharav and not their shadow as in the previous graphs (fig. 1.1-1.6). Fig. 3 gives a Solo Explorer sample giving the fundamental frequencies (Y-axis) against onset (X-axis).
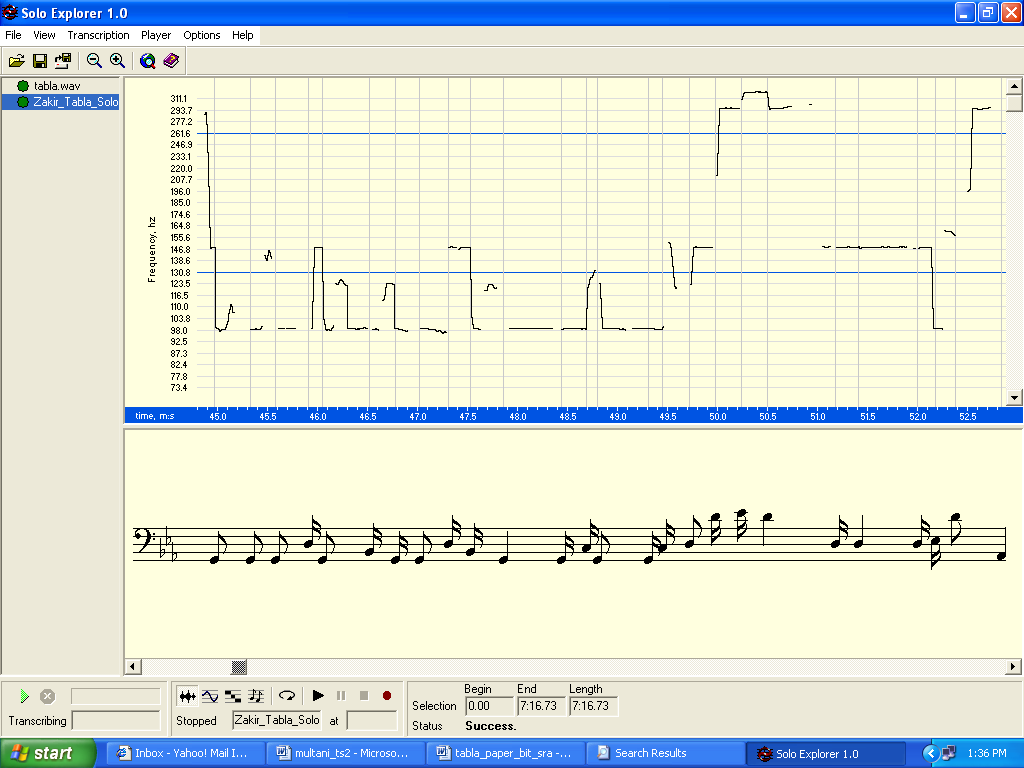
Tables 1, 2 and 3 give three samples of the text file generated by Solo Explorer giving digital values of fundamental frequencies in Hertz against onset (divide each onset value in first column by 100 to get time in seconds.
Table 1: First text sample of Solo Explorer (fundamental frequency ff against onset)
Onset ff
156 0.00 (remark: 156 implies 1.56 sec)
157 0.00
158 0.00
159 62.16
160 62.20
161 62.20
162 62.20
163 62.09
164 61.99
165 61.99
166 61.95
167 61.91
168 61.91
169 61.91
170 61.91
171 61.91
172 61.88
173 61.88
174 61.88
175 61.88
176 61.88
177 61.88
178 61.91
179 61.91
180 61.91
181 61.91
182 61.88
183 61.88
184 61.84
185 61.84
186 61.84
187 61.88
188 61.84
189 61.84
190 61.81
191 61.77
192 61.77
193 61.77
194 61.81
195 61.81
196 61.77
197 61.70
198 61.81
199 61.88
200 61.84
201 61.81
202 0.00
203 0.00
204 0.00
205 0.00
206 0.00
Table 2: Second text sample of Solo Explorer (fundamental frequency ff against onset)
Onset ff
228 0.00
229 0.00
230 0.00
231 223.07
232 222.81
233 222.68
234 222.68
235 222.43
236 222.30
237 222.43
238 222.30
239 222.17
240 222.43
241 222.30
242 222.04
243 222.43
244 222.30
245 221.91
246 222.17
247 222.43
248 222.30
249 222.17
250 221.91
251 221.79
252 221.91
253 222.04
254 221.91
255 221.66
256 221.79
257 221.91
258 222.04
259 0.00
260 0.00
261 0.00
262 0.00
263 0.00
264 0.00
265 0.00
Table 2: Second text sample of Solo Explorer (fundamental frequency ff against onset)
495 0.00
496 0.00
497 0.00
498 0.00
499 0.00
500 0.00
501 186.71
502 186.71
503 186.61
504 186.50
505 186.61
506 186.50
507 186.39
508 186.28
509 186.18
510 186.18
511 186.18
512 185.96
513 185.96
514 186.07
515 186.18
516 186.39
517 186.39
518 186.39
519 186.50
520 186.61
521 186.82
522 186.93
523 186.93
524 186.93
525 186.93
526 186.93
527 0.00
528 0.00
529 0.00
530 0.00
531 0.00
4. Melodic properties In order to find the melodic property we have calculated the timbre parameters of the tabla signal using Cool Edit and Wavesurfer package. The digitization of the signal was done at the rate of 22050 samples/sec (16 bits/sample). For more on timbre, see [11].
To study the melodic properties, timbre parameters which were analysed are as follows:
a) Brightness has a clear subjective meaning and contributes to the overall sound timbre and at the same time can be easily calculated on the basis of spectral properties [5,6].
![]()
where k is the partial index and ak is the amplitude of the k partial. A closely related attribute is sharpness [7], which, like the brightness, correlates with the perception of brightness.
b) Tristimulus values have been introduced in [7] as a timbre equivalent to the color attributes in the vision. The tristimulus is used in [8] to analyze the transient behavior of musical sounds which are defined as [5] (where partial 1 is the fundamental),



It is advantageously plotted in a diagram where tristimulus 2 is a function of tristimulus 3. In such a diagram, the three corners of the low left triangle denote strong fundamental, strong mid-range, and strong high frequency partials.
c) Odd/Even Relation is well known by [5],

To avoid too much correlation between the odd parameter and the tristimulus 1 parameter, the odd parameter is calculated from the third partial.
d) Irregularity: Several studies have pointed at the importance of the irregularity of the
![]()
spectrum [10].
e) Inharmonicity is another interesting parameter is the inharmonicity of the partial [10] Inharmonicity for each partial is defined as hn=mod(fn-n.fo)/(n.fo) where fn is the frequency of the partial, n is the number of partial and fo is the frequency of the fundamental. The inharmonicity of a complex tone is given by the sum of the inharmonicity of the partial.
f) Spectral Centroid of a sound is a concept adapted from psychoacoustics and music cognition. It is often used as a measure of ?gbrightness?h in comparing sounds. The higher is the centroid the brighter is the sound. It measures the average frequency, weighted by amplitude, of a spectrum. The standard formula for the (average) spectral centroid of a sound is [8,9,10]:
![]()
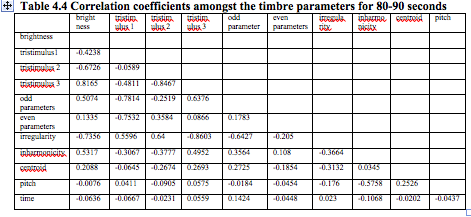
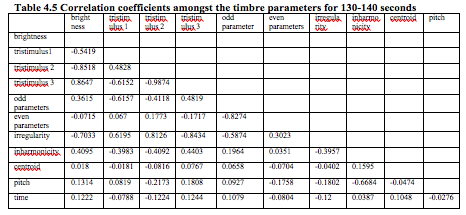
where ci is the centroid for one spectral frame, and i is the number of frames for the sound. The (individual) centroid of a spectral frame is defined as The timbre parameters as mentioned above were calculated and have been plotted in the graphs (Fig 4.1 to 4.9), pitch (fig 4.10) and time of each stroke (fig 4.11) for sets of interval 10 seconds i.e. on set 20-30 seconds, 50-70 seconds, 80-90 seconds, 130-140 seconds and 160-170 seconds as shown in the following figures.
![]()


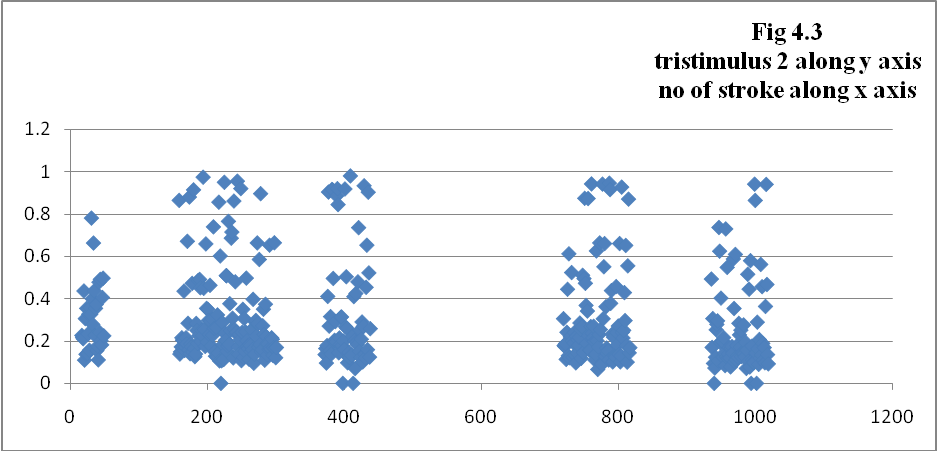


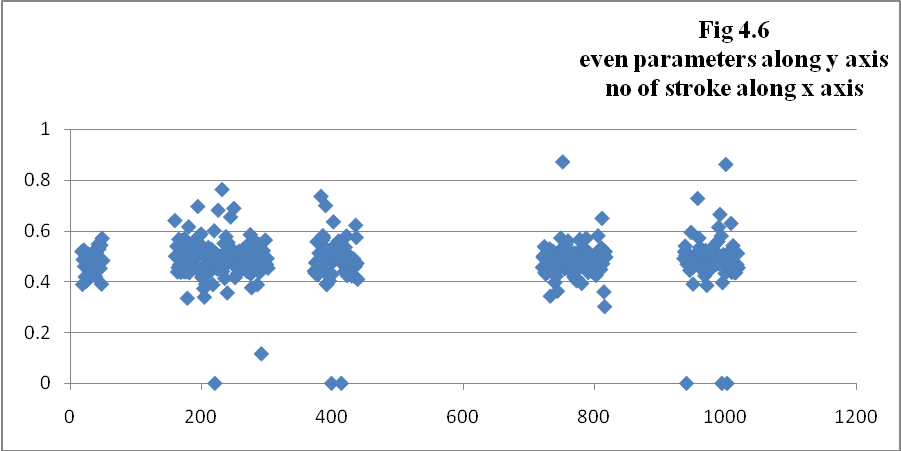
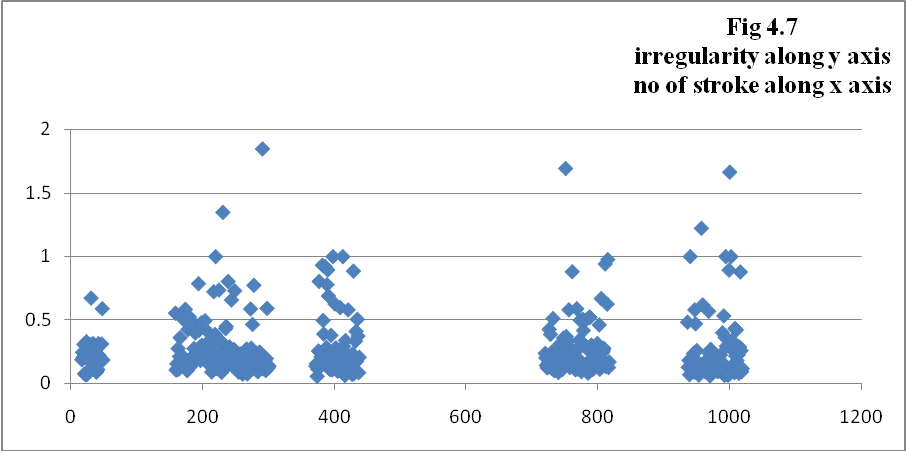
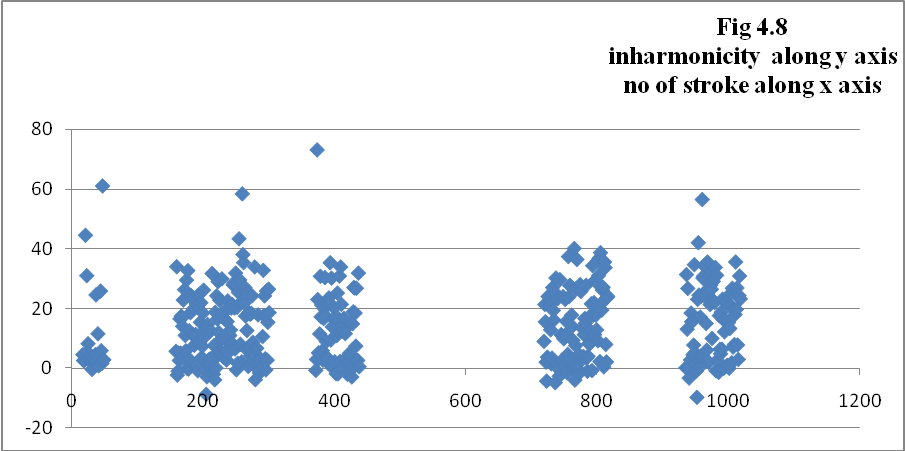


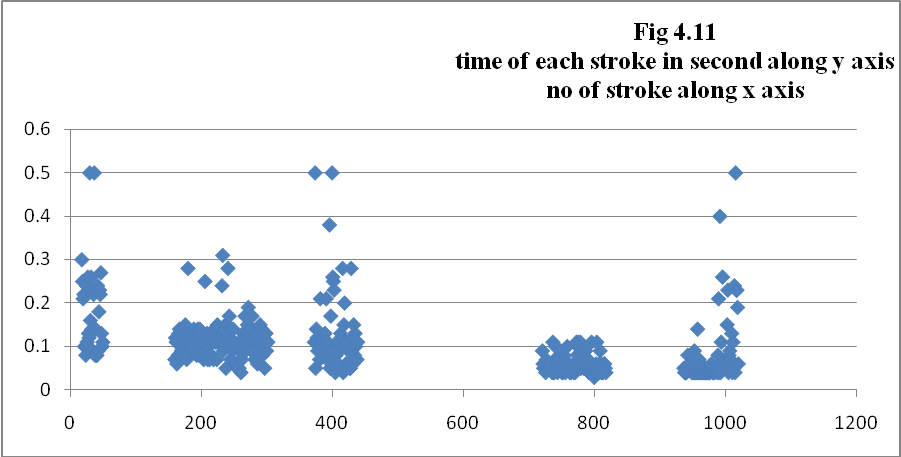
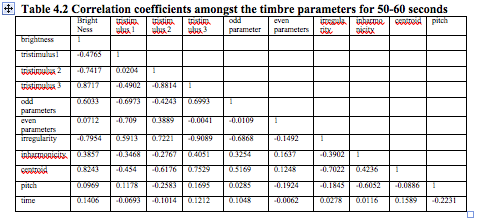
Table 4.1 Correlation coefficients amongst the timbre parameters for 20-30 seconds




5. Conclusion
In the light of our findings, we make the following concluding remarks:-
1. The shadow analysis describes the onsets of rise of the hand to a peak before dropping to strike the instrument as compared to metric and melodic analysis describing only metrical and melodic properties at the onsets of actual strikes.
2. Whether it is a rhythm or?gfiller?h (bharav) being depicted, from the analytical perspective, both studies are valuable.
3. The timbre analysis shows a formation of clusters reflecting the melodic and rhythmic properties at the onsets of actual stroke. This can be compared with the linearity of the shadow graphs.
4. The timbre parameters are highly correlated at the onset of actual stroke especially the brightness is highly correlated with tristimulus values, irregularity and inharmonicity. Brightness also shows a strong correlation with spectral centroid except during the second minute performance.
5. Tristimulus values are also highly correlated with other timbre parameters.
6. Irregularity and inharmonicity also shows high correlation with other parameters.
7. It is clear from the table 4.7 that the centroid, odd and even parameters and brightness shows very low dispersion of the partials from the average values. This also depicts the rhythm in the signal.
8. Fillers are being used by the musician to articulate a rhythm.
9. The above results show the presence of rhythmic property in the onset of stroke and in the onset of hand picking in the shadow.
Limitations of our methods:
1. Perhaps the ideal method of doing a shadow analysis would be to empirically analyze a video recording of a percussion performance. Unfortunately, the present recording is an audio sample. We are trying to procure video samples from the internet and other sources. The strength of our technique, however, lies in that those music samples for which only audio is available (the ones by old maestros who are no more deserve a special mention) must be analyzed this way. We are able to detect where there is a filler and where there is not. The shadow graph in the absence of fillers causes no problem. It is only the presence of fillers that creates the imbroglio. Given that the force with which the instrument is struck depends on the maximum peak of the hand before dropping, it might be of interest to draw a graph of loudness (measured by amplitude in volts) at the onset. We would call such a graph an analogue to shadow graph based on time. This is reserved as a rewarding future work which must be compared with the video analysis.
2. The melody analysis of a percussion is heavily dependent on timbre and timbre analysis has its own limitations. Timbre is defined as the quality of sound by which a sound signal produced by tabla (say) is distinguished from the one produced by a drum even if both have the same pitch and loudness. The definition tells what timbre is not and we learn it is neither pitch nor loudness. But have we learnt what timbre is? Worse, the timbre measures do not change so much if the instrument is changed keeping the pitch fixed. Rather they have been found to change more when the pitch is varied by the same instrument! [5] On the other hand, interestingly, the human brain never fails to identify a musical instrument or voice and herein lies our biggest hope. The question of interest is: what parameters the brain is fixing to identify a tabla sound as a tabla sound and why these parameters are more reliable? We look forward to the neuro-scientists and their achievements to find the right answer, it is another matter that their analysis would be both complex and quite different from ours.
[Concluded]
6. Appendix
Since a musical rhythm is a repeating pattern of onsets, it is periodic with some period n. Of course, a musical piece can involve different rhythmic patterns, but it makes sense to stick to one at a time for analysis. Now consider any circle, with n points placed at equal distance around its circumference. A subset of k points out of n represents a rhythm with n pulses and k onsets. Next, connect pairs of consecutive points yielding a cyclic polygon. The Euclidean distance between two onsets is defined as the length of the cord joining the corresponding onset points. Such a Euclidean rhythm E (k, n) is called maximally even if the sum of all aforementioned pair wise Euclidean distances is maximized [2], [3]. According to Martin, Taslakian and Toussaint [2], the shadow operation if performed on a rhythm ?gincreases the evenness of the new rhythm. One question that comes to mind is: what happens to the sequence obtained when we continue to perform this operation on every rhythm resulting from the shadow of another? This geometric problem has been well investigated in the mathematics literature. The study of properties of sequences of polygons generated by performing iterative processes on an initial polygon P0 has received much attention, and the shadow operation is one of many operations that has been investigated. Perhaps the most studied sequence is the one sometimes referred to as Kasner polygons [1], [2].Given a polygon P0, the Kasner descendant P1 of P0 is obtained by placing the vertices of P1 at the midpoints of the edges of P0 (making P1 the shadow of P0). Let P0, P1, P2, . . . be a sequence of cyclic polygons such that the vertex set of Pi is the shadow of the vertex set of Pi?|1 for all integers i ??o 0. We say that Pi is the shadow polygon of Pi?|1. Hitt and Zhang [4] show that given any convex cyclic polygon P0, its shadow sequence converges to a regular polygon. From their proof, it follows that the area of each Pi is greater than or equal to the area of Pi?|1 for any i > 0, with equality only when Pi is regular?h. Martin, Taslakian and Toussaint [2] have supplied a simpler proof compared to that of Hitt and Zhang. We omit the details.
References
1. J. Rahn. Turning the analysis around: African-derived rhythms and Europe- derived music theory. Black Music Research Journal, 16(1):71?|89, 1996.
2. F. Gomez Martin, P. Taslakian and G. Toussaint, Evenness Preserving Operations on Musical Rhythms, Proc. of the 2008 CSE Conference, Montreal, Quebec, Canada, May 12-13, 2008
3. S. Chakraborty, Review of [2] published in Computing Reviews, Aug 05, 2008 (www.reviews.com)
4. R. Hitt and X.-M. Zhang. Dynamic geometry of polygons. Elemente der Mathematik, 56:21?|37, 2001
5. K. Jensen and G. Marentakis, Hybrid Perception, Papers from the 1st Seminar on Auditory Models, Lyngby, Denmark, 2001. 6. H.F.Pollard and E.V.Jansson, A tristimulus method for the specification of musical timbre, Acustica, Vol. 51, 1982.
7. A.H.Benade and S.N.Kouzoupis, The clarinet spectrum: Theory and experiment, J. Acoustical Society of America, 83(1), 1988.
8. D.I.Repetto and L.Polansky, Cendroid - A Spectral Centroid Filter, Bregman Electronic Music Studio, Dartmouth College, http://music.dartmouth.edu/, 1997.
9. J. Krimphoff, S. Mc. Adams and S. Winsberg, ?gCaracterisation du timbre des sons complexes?h. II Analyses acoustiques et quantification psychophysique, journal de Physique IV, Colloque C5, Vol 4, 1994.
10. Musical Instrument Timbre Classification with Spectral features- Giulio Agostini, Maurizio Longari and Emanuele Pollastri. EURASIP Journal on Applied Signal Processing 2003:1, 5-14.
11. J.Krimphoff, S.McAdams and S.Winsberg, Caracte?Lrisation du timbre des sons complexes. II Analyses acoustiques et quantification psychophysique, Journal de Physique IV, Colloque C5, Vol. 4, 1994.
12. http://en.wikipedia.org/wiki/Tabla
* 2Sandeep Singh Solanki, 3Anirban Patranabis, 3Dipak Ghosh, 4Ranjan Sengupta, 4Ashok Kumar Datta and 4Nityananda Dey 1Department of Applied Mathematics, BIT Mesra, Ranchi-835215, India 2, Department of Electronics and Communication Engineering, BIT Mesra, Ranchi-835215, India 3Sir C V Raman Centre for Physics and Music, Jadavpur University, Kolkata 700032, India 4 Scientific Research Department, ITC Sangeet Research Academy, Kolkata 700040, India